LoRA Explained: Tiny Tweaks, Powerful Adaptations

Fine-tuning large language models (LLMs) like LLaMA or GPT-3 can require billions of parameters, massive GPUs, and weeks of training. But what if you could achieve similar results by training just 0.1% of the parameters?

What LoRA (Low-Rank Adaptation) helps us do. LoRA is a fine-tuning technique used in machine learning that freezes the base language model and adds small trainable components (small matrices called A and B) into specific layers. These new layers learn task-specific behavior, allowing the model to adapt without updating the full neural network.

Simple Analogy to Understand LoRA

Imagine Abhishek relocating from India to North America. Suddenly, none of his appliances fit into the new outlets. He has two options:

• Rewire his entire home to match his Indian plugs (expensive and messy), or
• Just buy a few cheap plug adapters and keep using his appliances.

LoRA is like option #2.

Rather than retraining the whole model (like rewiring the house), LoRA inserts small adapters (low-rank matrices) that allow the model to adapt to a new task. It’s lightweight, non-invasive, and cost-effective, making it ideal for parameter-efficient fine-tuning.

Traditional Fine-Tuning vs. LoRA

Traditional fine-tuning of pre-trained neural networks involves modifying the entire set of model weights. It means changing the original weight matrix (W) and adding a change ΔW, resulting in an updated model expressed as (W + ΔW).

However, this approach requires significant computational resources and memory. It often doubles the model size, making it inefficient for resource-constrained environments.

LoRA takes a different approach. Rather than altering W directly, LoRA breaks down the changes (ΔW) into two low-rank matrices (Wₐ and W_b), which are significantly smaller and trained only during fine-tuning.

This method reduces the number of trainable parameters dramatically while still allowing the model to adapt effectively to new tasks, all without modifying the core model.

The Intrinsic Rank Hypothesis

LoRA builds on the intrinsic rank hypothesis, which suggests that meaningful model updates exist in a low-dimensional space. Training only the smaller matrices allows LoRA to optimize model training efficiency without compromising performance.

It makes LoRA in NLP and LoRA for LLaMA/GPT models highly popular in the AI and deep learning communities.

Visual Representation

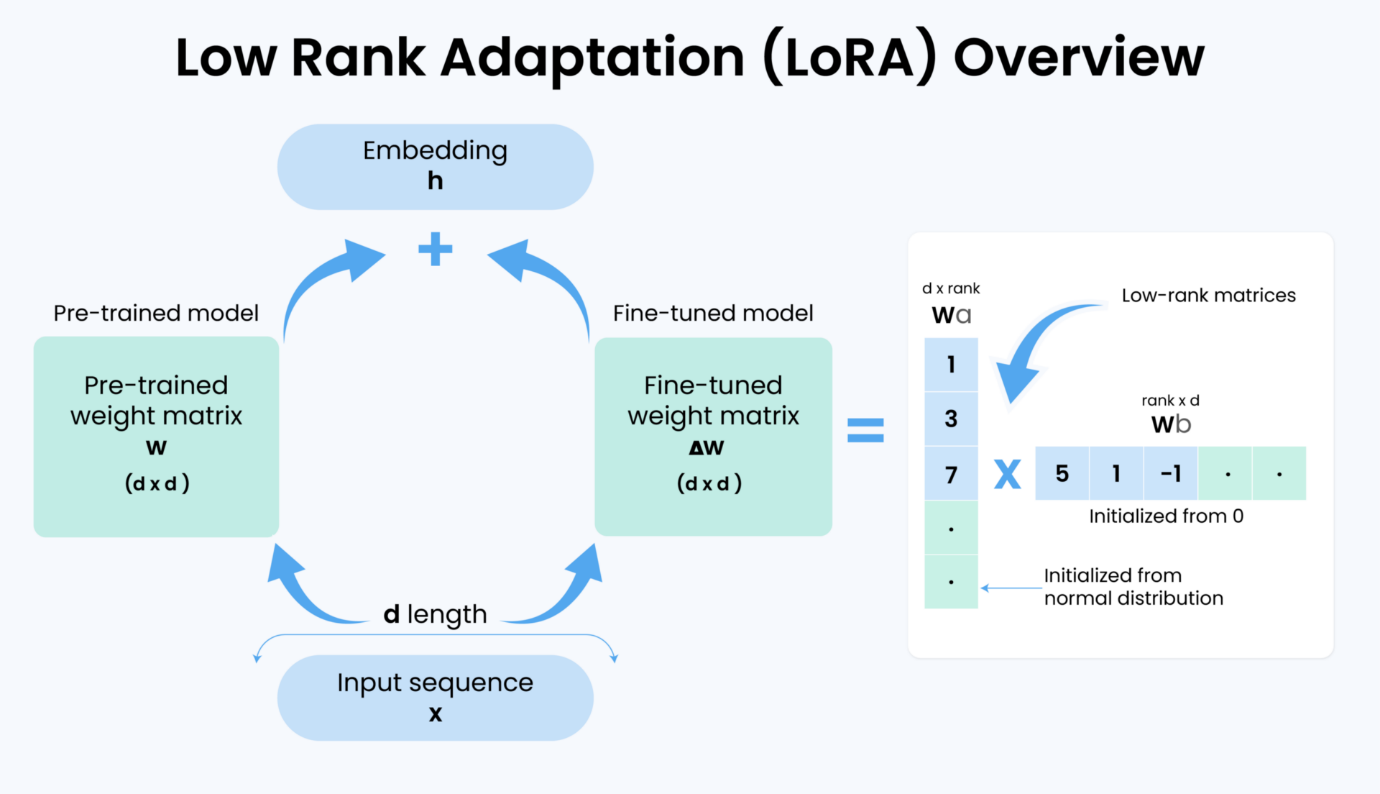
The image above illustrates how LoRA fine-tuning works. Instead of updating the full pre-trained weight matrix (W), LoRA keeps W frozen and learns a small matrix ΔW, decomposed into Wₐ and W_b (of dimensions d×r and r×d). This low-rank adaptation saves resources and maintains high performance.

Final Thoughts

Low-Rank Adaptation (LoRA) is an example of how a small but impactful change in deep learning model architecture can lead to significant improvements in performance and efficiency.

Whether working with large-scale LLMs, deploying on limited hardware, or experimenting with transfer learning techniques, LoRA provides a scalable and efficient solution.